興小弟讀書筆記

今天我們試著用小貓程式來求出兩數的最大公因數。

而輾轉相除法是歷史上最著名的演算法之一，是求兩數的最大公因數(GCD) 極快速的方法，故我們使用輾轉相除法來演算程式。

首先我們讓小貓程式可以輸入二個整數，先輸入大的整數，再輸入小的整數。

輸入整數之後，將該數新增至清單(陣列)之中，較大的整數新增至餘數A的清單，較小的整數新增至餘數B的清單。

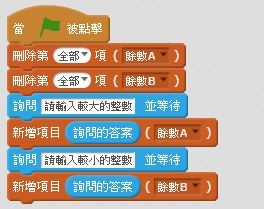
餘數A(陣列)中的第一項整數，設定給變數A，餘數B(陣列)中的第一項整數，設定給變數B。

整數A為較大之整數，故整數A為被除數，故將整數A除以整數B，取得餘數後設定給變數A。

以取得之餘數當做除數，再將整數B除以整數A，取得另一餘數後，將其設定給變數B。

如此重覆不停的做，直到A或B一數值等於0為止。

以下運算範例則為

一.整數A(12921)除以整數B(4234)，取得餘數219(商為3)。

二.整數B(4234)除以整數A(219)，取得餘數73(商為19)。

三.整數A(219)除以整數B(73)，取得餘數0(商為3)，故得知兩數最大公因數為73。

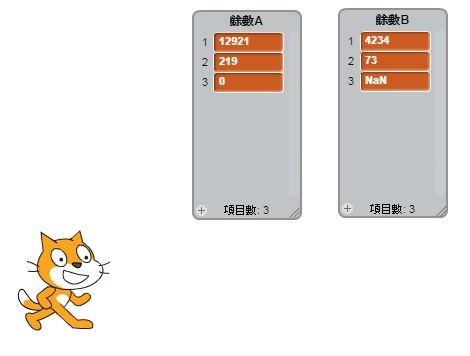
程式完成結果如下，輸入完畢後請按空白鍵執行程式
(建議使用Google Chrome瀏覽)